info@gerb.com
Estudio de caso de tecnologías de amortiguación para edificios altos: confort y seguridad
Directrices del Consejo de Edificios Altos y Hábitat Urbano (Council on Tall Buildings and Urban Habitat, CTBUH) sobre sistemas de amortiguación
Torre de pruebas de Thyssen Krupp, Rottweil (Alemania)
Datos del proyecto
- Año de finalización:
2016 (finalizado) - Promotor / contratista / propietario:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - Diseñador arquitectónico:
Arquitectos Werner Sobek y JAHN de Stuttgart y Chicago - Diseñador de estructuras:
Werner Sobek, Stuttgart - Proveedor de la amortiguación:
GERB Vibration Control Systems - Laboratorio de pruebas:
Wacker Ingenieure (Wind Engineering / Wind Tunnel Tests) - Altura / altura entre plantas:
246 m / 3,3 m (oficinas) - Relación de esbeltez:
1/11,8 - Plantas:
27 niveles / 8 plantas de oficinas - Superficie bruta de la torre:
340 metros cuadrados - Función del edificio:
Torre de pruebas de ascensores / oficinas / plataforma de observación (232 m) - Material de construcción:
Hormigón armado (C50/60) / fachada de membrana de PTFE sobre estructura de acero - Sistema estructural:
Núcleo de hormigón armado en voladizo sobre cimientos de losas
(–32 m) - Estrategia de amortiguación utilizada:
Sistema híbrido de amortiguación de masas (240 t)

1.0 Introducción, antecedentes
En el suroeste de Alemania, se ha erigido una torre de 246 m de altura para acoger un centro de pruebas de innovaciones para ascensores. La torre tiene una superficie circular de 20 m de diámetro y ofrece espacio para 9 huecos de ascensor de prueba, un ascensor de servicio contra incendios y un ascensor con vista panorámica de cristal. Además, se ha previsto un hueco de 220 m que se utilizará como hueco de elevación mecánica para garantizar los programas de pruebas.
La base de la torre tiene un diámetro de 40 m para disponer de espacio adicional para las instalaciones de servicio, un vestíbulo y un centro educativo. A una altura de 232 m, una plataforma de observación —la más alta de Alemania— permite disfrutar de una vista espectacular de la Selva Negra e incluso de los Alpes en días claros.

2.0 Sistema estructural
El sistema estructural de la torre de pruebas consiste básicamente en un tubo de hormigón armado de 20,8 m de diámetro que se hunde 30 metros en el suelo circundante (véase la figura 2). Hasta una altura de 110 m, el tubo tiene un espesor de 40 cm, por encima, de 25 cm. El suelo, compuesto por una capa de Keuper y piedra caliza de concha subyacente, proporciona una gran capacidad de carga, por lo que no fue necesaria la cimentación con pilotes. Además de la sujeción por el suelo circundante, la estructura más ancha de la base de la torre proporciona una rigidez lateral adicional.
La rigidez interna del tubo de hormigón se debe principalmente a las paredes interiores de los huecos de ascensor. Solo en determinadas alturas se instalaron losas de techo prefabricadas para permitir el acceso a los huecos de ascensor. Algunos de los huecos de ascensor terminan a una altura de 115 m y están cubiertos por suelos de vano largo de 40 cm de espesor que se colocaron allí mismo. Estas plantas están destinadas a oficinas. Por encima, hay un espacio vacío hasta la altura de 197 m que se utiliza como depósito de calor y para el sistema de TMD. La parte superior de la torre se destina a oficinas y al resto de los huecos de ascensor.

Una característica distintiva de la torre de pruebas es la fachada textil, que consiste en una malla de fibra de vidrio recubierta de PTFE. La anchura de la malla aumenta con la altura del edificio para potenciar la translucidez de la fachada, disminuir la densidad y el peso del material y lograr efectos aerodinámicos.
La forma de espiral de la fachada está concebida para funcionar como una espiral de Scruton y el propio tejido ayuda a dar sombra a la estructura de hormigón para evitar tensiones térmicas inducidas por la radiación solar. Para el diseño de la fachada y la elección del material, hubo que tener en cuenta algunos aspectos de la instalación, el mantenimiento y la durabilidad, así como la carga del viento.
3.0 Método de construcción

La torre de pruebas se construyó en las siguientes etapas:
- Excavación de un hoyo circular de 30 m de diámetro para la base de la torre. Tanto la excavación como la forma se lograron mediante una voladura inicial. Tras la excavación, el hoyo se aseguró con tirantes de anclaje y revestimiento de hormigón proyectado.
- Vertido de los cimientos de losas.
- Construcción de la estructura vertical de hormigón mediante encofrado deslizante. Todas las paredes se construyeron de forma continua durante un periodo de 4 meses.
- Construcción de las losas de forjado.
- Construcción de la zona de entrada.
4.0 Respuesta dinámica prevista a la carga del viento
Las frecuencias fundamentales para la torre de pruebas se predijeron en un intervalo de 0,17 Hz a 0,20 Hz en función de la etapa de construcción y del estado del hormigón (agrietado/sin agrietar), véase la figura 4.
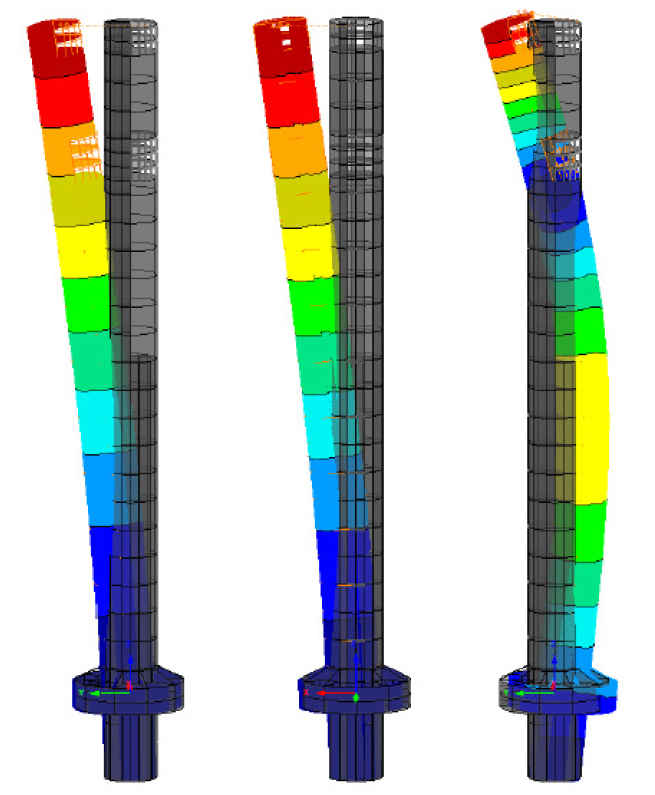
El análisis del viento reveló que podía producirse una excitación resonante de la estructura a velocidades de viento que correspondían a valores del suelo (altura de 10 m) del orden de 55 a 60 km/h. Se preveía que, sin una amortiguación adicional, esta excitación resonante provocaría deflexiones en la parte superior de +/-750 mm, lo que no solo causaría molestias a los ocupantes, sino que también tendría importantes repercusiones en la fatiga de la estructura de hormigón de la torre (véase la figura 5). Para reducir la respuesta dinámica a la excitación del viento cruzado, se utilizó un sistema pasivo de amortiguadores de masas sintonizadas. Como la torre se iba a utilizar como torre de pruebas para construir equipos de ascensores sensibles a las oscilaciones, el propietario buscaba la posibilidad de
someter la torre a una excitación artificial en días de calma, pero con desplazamientos que no causaran problemas de fatiga. El grado de movimiento de balanceo artificial solicitado se encontraba en el margen que se considera seguro de +/-200 mm. Esta solicitud dio la rara oportunidad de instalar un amortiguador de masa híbrido (HMD) o, dado que el sistema diseñado se desviaba de otros sistemas HMD instalados en el pasado, un denominado TMD de doble uso. El sistema se presentará en los siguientes capítulos, al igual que la optimización del sistema pasivo, el diseño del mecanismo de los actuadores, los algoritmos de control y el concepto de seguridad.

5.0 Optimización del sistema pasivo de amortiguadores de masas sintonizadas
Los parámetros del sistema de TMD pasivo debían determinarse teniendo en cuenta tres aspectos diferentes: a) proporcionar suficiente amortiguación estructural adicional para reducir la respuesta dinámica debida a la excitación por desprendimiento de vórtices, b) limitar el desplazamiento de la masa principal del TMD resultante en el modo pasivo a un valor alcanzable/práctico para cuando se vea sometido a una excitación por ráfagas de viento cruzado y c) elegir la masa del TMD en función del aporte de energía necesario para lograr la deflexión máxima deseada de la torre en el modo de excitación teniendo en cuenta la envolvente de rendimiento que permiten los actuadores suministrados
(es decir, la fuerza máxima generada y la carrera máxima durante el funcionamiento). Para optimizar el sistema de TMD se utilizó un modelo numérico que representaba la distribución de la masa de la torre y los momentos de inercia de la masa según las propiedades estructurales identificadas. También se adaptaron los elementos de rigidez entre las plantas para que coincidieran con las formas modales y las frecuencias naturales de las observaciones a tamaño real. En la figura 6 de la izquierda se muestran las formas modales y las frecuencias naturales del modelo análogo empleado. En la figura 6 de la izquierda también se comparan las formas modales del modelo análogo con las del modelo detallado preparado por el asesor de estructuras.
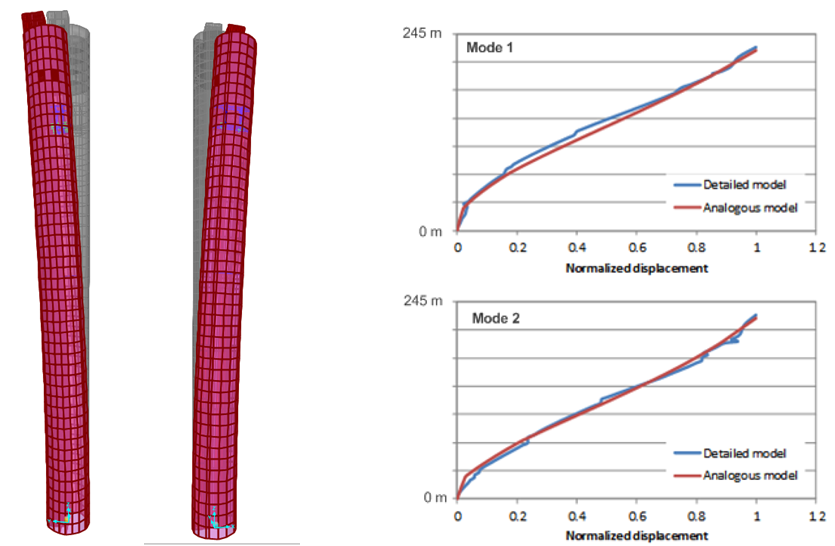
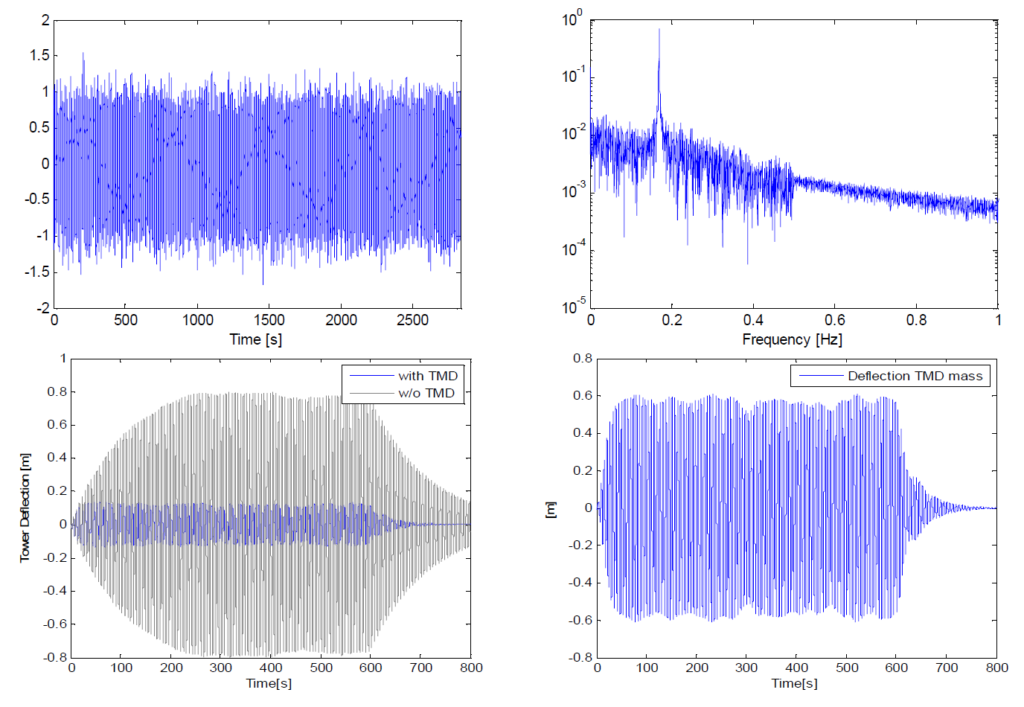
Además, el TMD se modeló de forma diferenciada como un sistema pendular y teniendo en cuenta su posición excéntrica en la torre. Las características de carga para el caso de aportación dominante, es decir, la excitación resonante debida al desprendimiento de vórtices, son muy parecidas a las de una excitación armónica simple. Aun así, la carga de ráfaga coexistente es de naturaleza intrínsecamente estocástica, por lo que se aplican criterios de optimización distintos del conocido criterio de Den Hartog. Además, los desplazamientos relativos de la masa del TMD son mayores para una carga estocástica que para una carga de tipo armónico. Puesto que para la determinación numérica de los parámetros óptimos del TMD debe considerarse una carga cercana a la realidad, se generó un histórico temporal que incluía tanto la carga estocástica de ráfagas (basada en el espectro de Davenport) como una componente resonante superpuesta, similar al desprendimiento de vórtices, para representar la excitación general del viento cruzado (véase la fig. 3 derecha). En la figura 3 derecha se muestra la reducción de la deflexión de la torre que se puede lograr con el sistema de TMD pasivo, así como los desplazamientos de TMD resultantes.
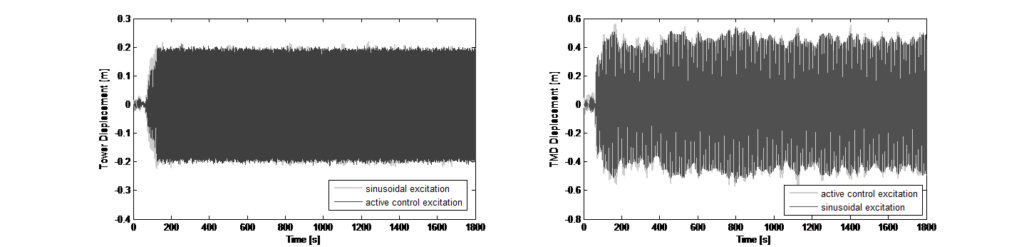
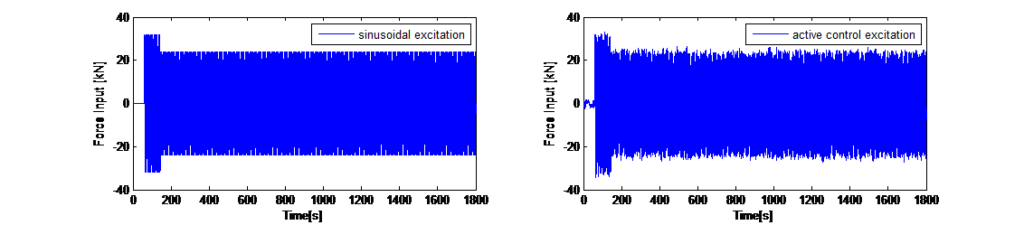
A partir de estos resultados, para una amortiguación estructural inherente estimada de ξ=0,8 %, se determinó que el TMD debía tener una masa de 240 t para mantener los desplazamientos dentro de +/-650 mm y, al mismo tiempo, mantener una relación de amortiguación del TMD óptima para obtener el mejor rendimiento del TMD. Un incremento de la amortiguación del TMD podría haber reducido el desplazamiento sin que por ello la eficacia dejara de ser suficiente, pero esto habría afectado negativamente a los requisitos de fuerza del actuador. Para determinar las fuerzas necesarias para la configuración óptima del TMD de 240 t, se utilizó también el modelo análogo para constatar que, con una fuerza máxima de 40 kN de los actuadores, se pueden lograr deflexiones de la torre en el margen de +/-200 mm. En la figura 4 se muestran los resultados de una simulación numérica en el dominio del tiempo sobre el modelo numérico análogo; para ello, se muestran las deflexiones resultantes de la parte superior de la torre, las deflexiones de la masa del TMD y las fuerzas activas de entrada que las provocan.


6.0 Descripción del sistema de control
La dualidad del sistema de control tiene como objetivo a) reducir el consumo de energía durante el funcionamiento pasivo normal para disminuir las vibraciones que se producen y b) reducir los requisitos de fuerza de los actuadores al utilizar los efectos de resonancia con el fin de excitar la masa principal del TMD y lograr finalmente la demanda de fuerza real. Por lo tanto, en comparación con otros sistemas de control (véase la fig. 1), los actuadores conectan la estructura principal y la masa del TMD, pero no se utilizan para controlar la masa del TMD directamente, como sería el caso de un sistema de conductor/amortiguador de masa activa típico.
Para el TMD de doble uso instalado, se eligió una masa de reacción para el funcionamiento pasivo de 240 toneladas. Para el modo de funcionamiento de excitación, se acoplaron dos accionamientos lineales a la masa del TMD —uno en cada dirección principal— con pivotes cerca del centro de gravedad de la masa para evitar cualquier artefacto de torsión. Cada accionamiento lineal puede proporcionar fuerzas de hasta 40 kN dentro de una carrera de como máximo +/-600 mm (véase el detalle en la fig. 2). Los accionamientos lineales se pueden desmontar para que el modo pasivo no se vea influenciado por los rodamientos de los actuadores en el improbable caso de que se produzca un fallo en ellos.
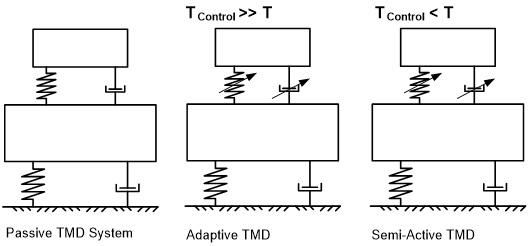
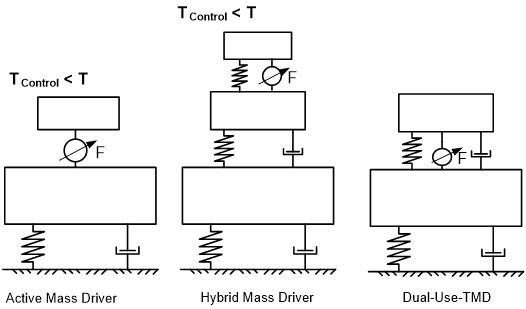
Figura 10: Tipos de sistemas de control, comparación del TMD de doble uso con sistemas pasivos, semiactivos, activos e híbridos
El sistema está equipado con cuatro acelerómetros uniaxiales (K-Beam sísmico/MEMS; uno en cada dirección) para determinar el nivel superior de la torre y las aceleraciones de la masa del TMD. Las señales de aceleración se filtran por paso de banda en la gama de frecuencias naturales fundamentales de la torre (0,1 a 0,3 Hz) y se integran para obtener las velocidades y deflexiones de la torre.
Además, los valores de desplazamiento integrados pueden compararse con los de un sistema global de navegación por satélite complementario instalado también en la parte superior para comparar las derivas de la señal. Para ello, se realizó una primera prueba de correlación. Por otra parte, los desplazamientos del TMD son controlados directamente con transductores de potencia de cuerda y un sistema inductivo de medición de longitudes integrado en los motores lineales.
7.0 Algoritmo de control
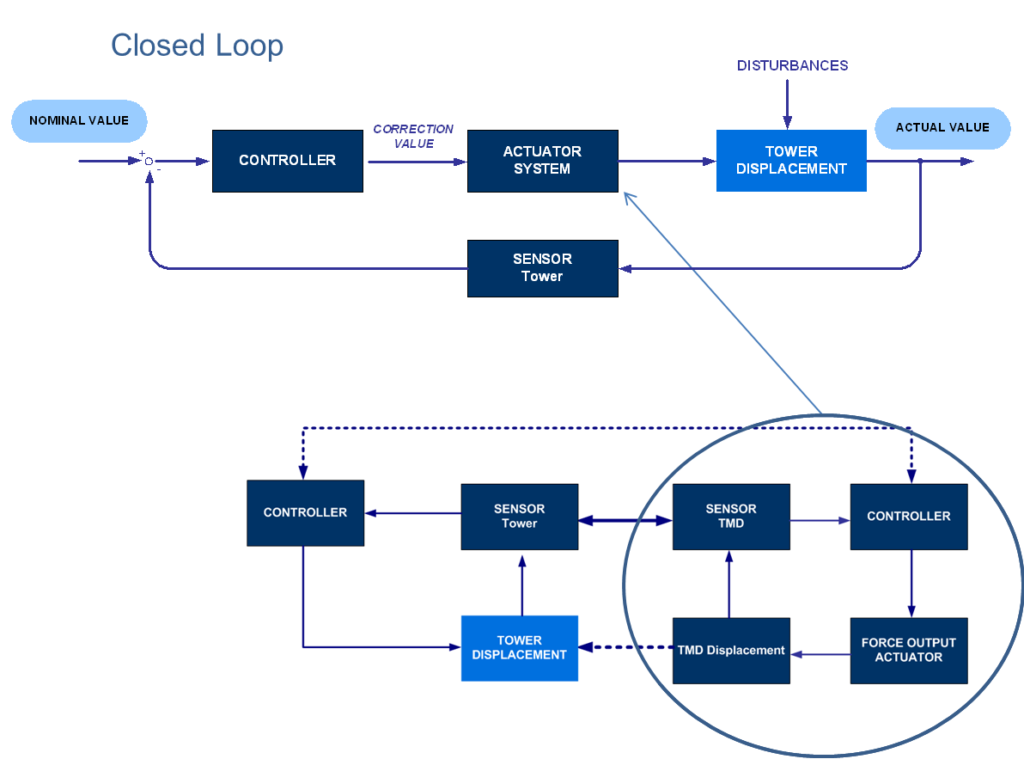
El bucle de control general para la torre se muestra en la figura 5, donde se ilustra la secuencia de control en bucle cerrado. El diseño detallado del algoritmo de control requeriría modelos analíticos de la interacción entre los actuadores y la masa del TMD para determinar la conexión entre la entrada del actuador y la fuerza de acción aplicada. Estos deberían combinarse con el modelo analítico de la estructura principal que describe el comportamiento dinámico general del edificio. Además, en comparación con los algoritmos de control estándar que se utilizaron en otras aplicaciones de HMD como en [2],[3] o que se analizaron de manera teórica como en [1] el algoritmo de control para esta torre tuvo que tener en cuenta la excitación sincrónica controlada en una dirección principal y la reducción de la vibración en la dirección perpendicular. Dado que se espera que la respuesta dinámica se produzca principalmente en los modos fundamentales, podría aplicarse un control de retroalimentación lineal, con todas sus ventajas, para estas dos tareas a fin de evitar inestabilidades. Para llevar a cabo el control simple, el control de retroalimentación lineal, que atenúa la respuesta dinámica de las torres de forma perpendicular a la excitación, acciona el actuador correspondiente mediante una suma lineal ponderada especificada de siete mediciones dinámicas estructurales. Estas mediciones son: las aceleraciones del TMD y de la parte superior de la torre, las velocidades del TMD y de la parte superior de la torre, los desplazamientos del TMD y de la parte superior de la torre y el desplazamiento relativo del TMD a la parte superior de la torre.
Es importante señalar que los factores de ponderación preseleccionados son ganancias escalares simples, positivas o negativas. La parametrización de los factores de ponderación se basa en las pruebas dinámicas de la torre y no se aplica ninguna modificación dependiente de la frecuencia. La retroalimentación del actuador activo se calcula de manera instantánea (a 50 Hz) y es de nuevo una combinación lineal de las mediciones dinámicas anteriores. No se utiliza ninguna manipulación no lineal. El diseño de control también se puso a prueba en una simulación numérica en el dominio del tiempo (es decir, integración directa) para comprobar el rendimiento de la mitigación de las vibraciones del control del actuador. Para el modo de excitación se utilizó el mismo enfoque de control en combinación con un desplazamiento que representa la excitación de la torre hasta el valor de desplazamiento deseado. El desplazamiento es una función sinusoidal basada en la frecuencia fundamental captada en cada dirección. La salida de control destinada a contrarrestar la variación del desplazamiento superior debida a otras perturbaciones se modula entonces sobre la función de desplazamiento sinusoidal y el valor de control se adapta en consecuencia.
El control de retroalimentación lineal que reduce la respuesta dinámica de las torres de forma perpendicular a la excitación permite que la orden de fuerza para el actuador sea una suma lineal ponderada especificada de las siete mediciones dinámicas del programa. Estas siete mediciones son la aceleración del TMD y de la torre, la velocidad del TMD y de la torre, el desplazamiento del TMD y de la torre y el desplazamiento relativo del TMD a la torre. Es importante señalar que los factores de ponderación son valores escalares simples, positivos o negativos. La parametrización del factor de ponderación se basa en las pruebas dinámicas experimentales de la torre. La retroalimentación del actuador es activa y se calcula de forma instantánea (50 Hz),
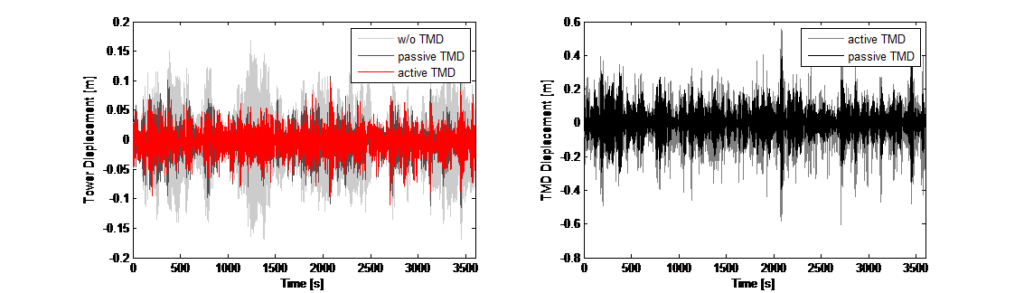
mientras que los factores de ponderación son escalares y no utilizan ninguna forma de función de transferencia dependiente de la frecuencia. Además, la retroalimentación es una combinación lineal de la propiedad dinámica. No se aplica ninguna manipulación ni lógica no lineal. El diseño de control se desarrolló para una simulación numérica en el dominio del tiempo (integración directa), de manera que la entrada de fuerza se pudiera adaptar a la masa del TMD como control del actuador para cada paso de tiempo. En la figura 12 se muestran los resultados de la simulación para la supresión de vibraciones, los desplazamientos de la torre y el recorrido resultante de la masa del TMD.
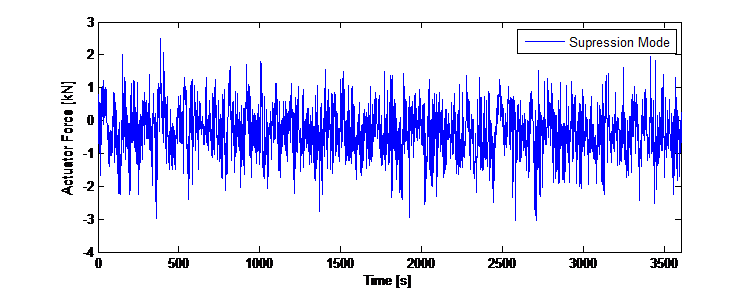
Para el modo de excitación se utilizó el mismo enfoque de control en combinación con un desplazamiento que representa la excitación de la torre hasta el valor de desplazamiento deseado. El desplazamiento es una función sinusoidal basada en la frecuencia fundamental captada en cada dirección. La salida de control destinada a contrarrestar la variación del desplazamiento superior debida a las perturbaciones se modula entonces sobre la función de desplazamiento
sinusoidal y el valor de control se adapta en consecuencia. Para este desplazamiento se determinó un factor de ponderación experimental. En la figura 13 se muestran los resultados numéricos con la perturbación de la carga de ráfagas para el modo de excitación con una excitación sinusoidal simple y con la aplicación del algoritmo de control.
8.0 Concepto de seguridad
Teniendo en cuenta la fuerza de +/-40 kN que pueden proporcionar los accionamientos lineales que se utilizan como actuadores, es indispensable contar con un concepto de seguridad que garantice que los desplazamientos de la torre no superen las previsiones de fatiga. Esto es aplicable incluso aunque la salida de fuerza no sea suficiente para causar deflexiones superiores a los +/-200 mm predeterminados. Un modo de mejorar la seguridad del sistema era aumentar la redundancia de los sensores de control que registran la deflexión superior de la torre. La mejor manera de lograrlo es mediante un sistema de control adicional e independiente que, en el mejor de los casos, utilice un principio de medición diferente al del hardware de control. Para el proyecto que aquí se presenta, el hardware de control utilizó, como ya se ha mencionado, acelerómetros y un umbral de aceleración definido para el filtrado de paso de banda de la señal dentro del intervalo de las frecuencias naturales relevantes de la estructura. El sistema de control superior es un sistema global de navegación por satélite (GNSS, por sus siglas en inglés) con una precisión de +/-10 mm.
Para el GNNS se necesita una estación base de referencia, que procesa los datos de coordenadas a los valores de respuesta de desplazamiento reales. Si el desplazamiento superior de la torre supera un umbral predeterminado durante el modo de excitación artificial, lo que podría deberse a un viento adicional u otra excitación, un relé cambiará la señal a 0 V. Esto provocará la interrupción del modo de excitación. Además, ambos sistemas de control comprueban constantemente los datos obtenidos en busca de señales erróneas de los sensores, lo que también provocará la interrupción del modo de excitación activo. Las señales de aceleración/potencia erróneas se detectarán mediante un criterio de detección de picos espectrales; solo podrá asumirse que los sensores proporcionan señales legítimas si es posible detectar picos en un margen relevante. Cuando el GNNS analiza el cambio de los datos de coordenadas, si los datos recogidos no cambian en el momento oportuno, se asumirá automáticamente que la señal es errónea.
9.0 Pruebas de vibración
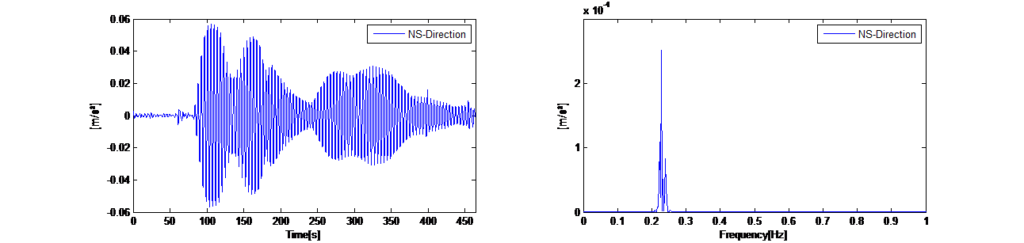
Las pruebas de vibración iniciales de la torre se efectuaron en la fase actual, en la que la torre aún no está terminada, por lo que las frecuencias fundamentales de la torre en esta fase están por encima del margen de sintonización especificado en el sistema de TMD pasivo. El TMD está adaptado a la frecuencia de sintonización más alta posible. El objetivo de las pruebas de vibración era determinar las frecuencias fundamentales de la torre con el sistema de TMD bloqueado, así como la amortiguación estructural inherente. También debía determinarse el comportamiento dinámico con el sistema TMD pasivo acoplado, así como el aumento de la amortiguación estructural debido al sistema de TMD pasivo. Para identificar las frecuencias naturales fundamentales de la torre se puede utilizar el método de la densidad espectral de potencia normalizada promediada [1] (ANPSD, por sus siglas en inglés). Para ello, es necesario separar en segmentos los históricos temporales registrados. Estos segmentos deben transformarse en el dominio de la frecuencia. Los espectros obtenidos deben normalizarse, promediarse y multiplicarse por el espectro complejo conjugado.
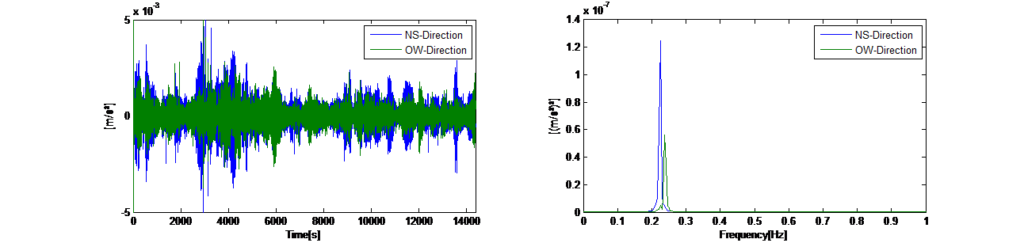
De este modo, se eliminarán todas las vibraciones aleatorias y solo se mostrarán las vibraciones libres recurrentes de la estructura en el espectro promediado, que ahora representa las frecuencias naturales excitadas de forma dominante en la torre. En la figura 14 izquierda se muestran los históricos temporales registrados de las vibraciones ambientales horizontales en las direcciones x e y con el TMD bloqueado. En la figura 14 derecha se muestran los espectros de potencia automática promediados obtenidos para una longitud de segmento de 120 s. Los espectros indican que la torre presenta una respuesta dinámica en dos frecuencias dominantes (0,225 Hz en la dirección x y 0,245 Hz en la dirección y).
Además del método del espectro de potencia promediado descrito anteriormente —que parte del supuesto de que la excitación ambiental provoca una respuesta dinámica suficiente en los modos de vibración de interés para obtener seguridad estocástica—, las frecuencias naturales se determinaron con el software comercial de procesamiento de señales ARTEMIS, [1] que incorpora el método de descomposición mejorada en el dominio de la frecuencia y el de identificación del subespacio estocástico.
La descomposición mejorada en el dominio de la frecuencia (EFDD, por sus siglas en inglés) y la identificación del subespacio estocástico son técnicas ampliamente utilizadas para la identificación de parámetros modales solo de salida.
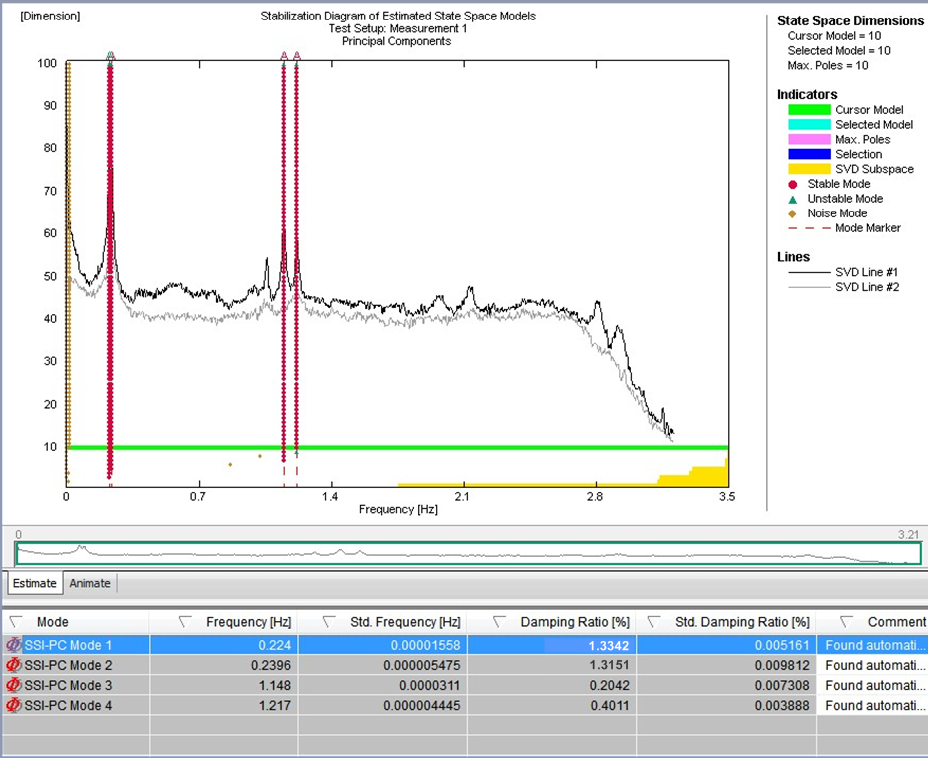
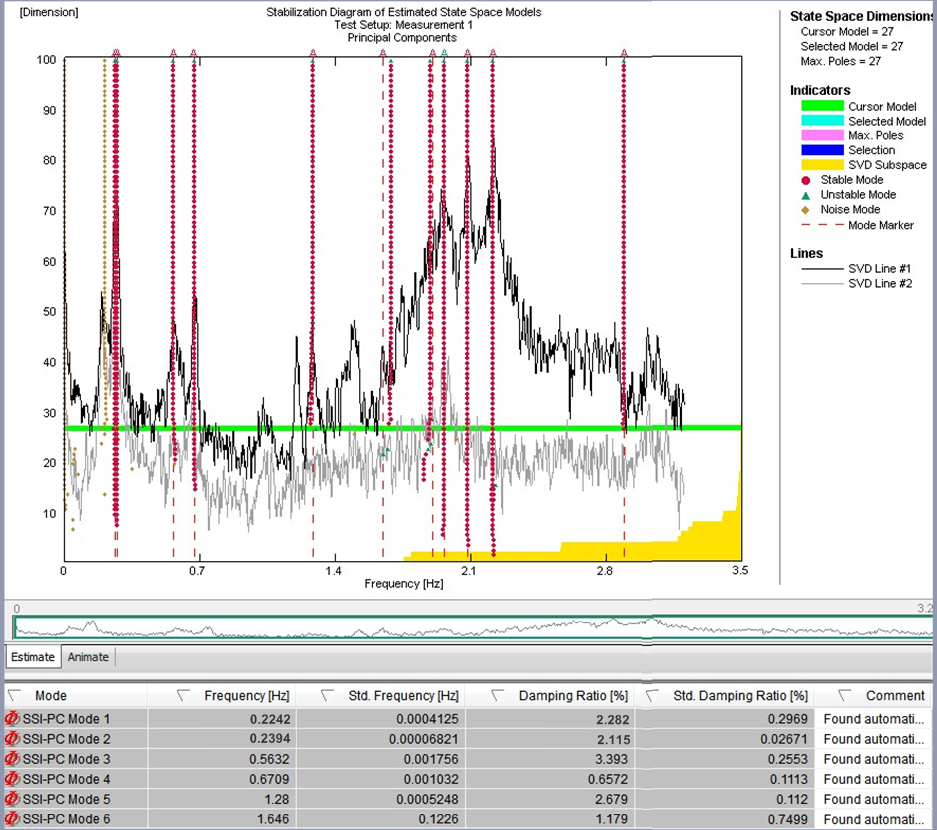
Figura 15: Tarjetas de estabilidad para el registro de la vibración ambiental con el TMD bloqueado (izquierda) y activado (derecha)
El método EFDD se basa en el cálculo de los espectros de respuesta. Por lo tanto, se necesitan registros extensos para mantener bajo el error en la estimación del espectro y para extraer los parámetros modales de forma fiable. El algoritmo de identificación del subespacio estocástico se aplicó para identificar los puentes con un modelo de solo salida. Los métodos de identificación del subespacio estocástico funcionan en el dominio del tiempo y se basan en una descripción del espacio de estados del problema dinámico. Los resultados de la identificación del sistema en diferentes órdenes del modelo se comparan para distinguir los verdaderos modos estructurales de los modos espurios en los denominados diagramas de estabilización. Estos diagramas son una forma popular de seleccionar el modelo del sistema identificado, ya que los modos estructurales verdaderos tienden a ser estables para órdenes de modelo sucesivos y cumplen determinados criterios de estabilización que se evalúan en un procedimiento automatizado. La figura 15 presenta la tarjeta de estabilidad correspondiente a los datos ambientales registrados, a partir de la cual se han podido determinar los modos pertinentes. En la figura 14 también se muestran los modos identificados y las relaciones de amortiguación determinadas para cada modo con el TMD bloqueado (izquierda) y el TMD activado (derecha). Se observa un aumento de la amortiguación estructural. La amortiguación estructural adicional está en el intervalo de un valor teórico que puede determinarse a partir del modelo teórico para el que se consideró la configuración del TMD desintonizado.
Además de las pruebas de vibración ambiental con el sistema de TMD pasivo, se realizaron pruebas preliminares con el modo de excitación activo a pesar del estado desintonizado del sistema de TMD. En la figura 12 izquierda se muestra el histórico temporal de las aceleraciones registradas en la parte superior de la torre. Después de una excitación sinusoidal inicial, se habilitó el algoritmo para un grado de aceleración constante con el fin de determinar de forma experimental la correlación existente entre la deflexión de la torre y el desplazamiento forzado de la masa del TMD. El histórico temporal que se muestra en la figura 12 presenta los dos escenarios de prueba en el modo de excitación, y los espectros FFT correspondientes indican la evidente respuesta de la torre en sus dos frecuencias fundamentales (dirección x e y). El tramo de tiempo marcado en verde corresponde a una excitación sinusoidal de la masa con el control activo desactivado que provocó una respuesta dinámica en ambas direcciones principales. El espectro FFT resultante indica los dos picos que identifican las frecuencias fundamentales en estas dos direcciones. El fragmento de tiempo marcado en azul corresponde a una excitación con control activo habilitado que provocó un desplazamiento de la torre más estable con predominio de una dirección. El decaimiento de la vibración resultante después de desactivar el modo de excitación también se utilizó para determinar la amortiguación estructural y se determinó que era D = 2,4 %. Este resultado coincide con la relación de amortiguación determinada con los algoritmos SSI.
10.0 Conclusión y perspectivas
En la torre de pruebas de Thyssen Krupp, de 246 m de altura, se instaló un TMD de doble uso con el objetivo de someter a la torre a una respuesta dinámica controlada en sus frecuencias fundamentales. El objetivo de esta excitación es lograr un balanceo definido del edificio en las dos direcciones principales de la torre. A partir de los cálculos numéricos se determinó que el TMD debía tener una masa de 240 t para lograr la amortiguación suplementaria necesaria para el modo pasivo y generar la fuerza de control necesaria para lograr el desplazamiento superior de la torre de +/-200 mm. Para generar un desplazamiento estable para el modo de excitación y suprimir los desplazamientos causados por el viento y la componente de vibración forzada en la dirección perpendicular, se desarrolló un algoritmo de control que se probó con simulaciones numéricas. Después de instalar el sistema de TMD de tipo péndulo pasivo, para el que se utilizaron losas de hormigón prefabricadas como masa de reacción, se pusieron en marcha los actuadores y se realizaron las primeras pruebas. Las pruebas revelaron que la amortiguación inherente de la torre era más alta de lo previsto, pero todos los modos relevantes pudieron determinarse con precisión. El modo de excitación activa del edificio funcionaba y pudo probarse, aunque no en toda su extensión para derivar todos los parámetros de funcionamiento, ya que el edificio aún no está totalmente terminado. Debido al estado prematuro del edificio, el TMD pasivo no pudo adaptarse a las frecuencias fundamentales determinadas.
Una vez adaptado el sistema TMD, se llevarán a cabo nuevas pruebas en el edificio, entre las que se incluirán también pruebas relativas a la amortiguación dependiente de la amplitud y a la integridad del concepto de seguridad.
REFERENCIAS
[1] Wenzel, H.; Pichler, D.; Schedler, R. (1991). «Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken», Bauingenieur 74
[2] Döhler, M.; Andersen, P.: Mevel, L. (2012). «Operational Modal Analysis using a Fast Stochastic Subspace Identification Method», Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T.; Spencer, J.R. (2000). «Active, Semi-Active and hybrid control of structures» In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199-1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437-446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655-1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24-29.
[8] Soong, T.T. «Active Structural Control: Theory and Practice»; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A.; Kazuto, S. (2008). «Active Control of Structures», Wiley, Padstow
Otros recursos
¿Desea recibir más información acerca de este tema?
Póngase en contacto con nosotros para hacernos llegar su consulta.
Uno de nuestros ingenieros de proyectos se pondrá en contacto con usted en breve.
Estudio de caso de tecnologías de amortiguación para edificios altos: confort y seguridad
Directrices del Consejo de Edificios Altos y Hábitat Urbano (Council on Tall Buildings and Urban Habitat, CTBUH) sobre sistemas de amortiguación
Torre de pruebas de Thyssen Krupp, Rottweil (Alemania)
Datos del proyecto
- Año de finalización:
2016 (finalizado) - Promotor / contratista / propietario:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - Diseñador arquitectónico:
Arquitectos Werner Sobek y JAHN de Stuttgart y Chicago - Diseñador de estructuras:
Werner Sobek, Stuttgart - Proveedor de la amortiguación:
GERB Vibration Control Systems - Laboratorio de pruebas:
Wacker Ingenieure (Wind Engineering / Wind Tunnel Tests) - Altura / altura entre plantas:
246 m / 3,3 m (oficinas) - Plantas:
27 niveles / 8 plantas de oficinas - Superficie bruta de la torre:
340 metros cuadrados - Función del edificio:
Torre de pruebas de ascensores / oficinas / plataforma de observación (232 m) - Estrategia de amortiguación utilizada:
Sistema híbrido de amortiguación de masas (240 t)

- Material de construcción:
Hormigón armado (C50/60) / fachada de membrana de PTFE sobre estructura de acero - Sistema estructural:
Núcleo de hormigón armado en voladizo sobre cimientos de losas
(–32 m)
Estudio de caso de tecnologías de amortiguación para edificios altos: confort y seguridad
Directrices del Consejo de Edificios Altos y Hábitat Urbano (Council on Tall Buildings and Urban Habitat, CTBUH) sobre sistemas de amortiguación
Torre de pruebas de Thyssen Krupp, Rottweil (Alemania)
Datos del proyecto
- Año de finalización: 2016 (finalizado)
- Promotor / contratista / propietario: Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators
- Diseñador arquitectónico: Arquitectos Werner Sobek y JAHN de Stuttgart y Chicago
- Diseñador de estructuras: Werner Sobek, Stuttgart
- Proveedor de la amortiguación: GERB Vibration Control Systems
- Laboratorio de pruebas: Wacker Ingenieure (Wind Engineering / Wind Tunnel Tests)
- Altura / altura entre plantas: 246 m / 3,3 m (oficinas)
- Plantas: 27 niveles / 8 plantas de oficinas
- Superficie bruta de la torre: 340 metros cuadrados
- Función del edificio: Torre de pruebas de ascensores / oficinas / plataforma de observación (232 m)
- Material de construcción: Hormigón armado (C50/60) / fachada de membrana de PTFE sobre estructura de acero
- Sistema estructural: Núcleo de hormigón armado en voladizo sobre cimientos de losas (–32 m)
- Estrategia de amortiguación utilizada: Sistema híbrido de amortiguación de masas (240 t)

1.0 Introducción, antecedentes
En el suroeste de Alemania, se ha erigido una torre de 246 m de altura para acoger un centro de pruebas de innovaciones para ascensores. La torre tiene una superficie circular de 20 m de diámetro y ofrece espacio para 9 huecos de ascensor de prueba, un ascensor de servicio contra incendios y un ascensor con vista panorámica de cristal. Además, se ha previsto un hueco de 220 m que se utilizará como hueco de elevación mecánica para garantizar los programas de pruebas.
La base de la torre tiene un diámetro de 40 m para disponer de espacio adicional para las instalaciones de servicio, un vestíbulo y un centro educativo. A una altura de 232 m, una plataforma de observación —la más alta de Alemania— permite disfrutar de una vista espectacular de la Selva Negra e incluso de los Alpes en días claros.

2.0 Sistema estructural
El sistema estructural de la torre de pruebas consiste básicamente en un tubo de hormigón armado de 20,8 m de diámetro que se hunde 30 metros en el suelo circundante (véase la figura 2). Hasta una altura de 110 m, el tubo tiene un espesor de 40 cm, por encima, de 25 cm. El suelo, compuesto por una capa de Keuper y piedra caliza de concha subyacente, proporciona una gran capacidad de carga, por lo que no fue necesaria la cimentación con pilotes. Además de la sujeción por el suelo circundante, la estructura más ancha de la base de la torre proporciona una rigidez lateral adicional.
La rigidez interna del tubo de hormigón se debe principalmente a las paredes interiores de los huecos de ascensor. Solo en determinadas alturas se instalaron losas de techo prefabricadas para permitir el acceso a los huecos de ascensor. Algunos de los huecos de ascensor terminan a una altura de 115 m y están cubiertos por suelos de vano largo de 40 cm de espesor que se colocaron allí mismo. Estas plantas están destinadas a oficinas. Por encima, hay un espacio vacío hasta la altura de 197 m que se utiliza como depósito de calor y para el sistema de TMD. La parte superior de la torre se destina a oficinas y al resto de los huecos de ascensor.

Una característica distintiva de la torre de pruebas es la fachada textil, que consiste en una malla de fibra de vidrio recubierta de PTFE. La anchura de la malla aumenta con la altura del edificio para potenciar la translucidez de la fachada, disminuir la densidad y el peso del material y lograr efectos aerodinámicos.
La forma de espiral de la fachada está concebida para funcionar como una espiral de Scruton y el propio tejido ayuda a dar sombra a la estructura de hormigón para evitar tensiones térmicas inducidas por la radiación solar. Para el diseño de la fachada y la elección del material, hubo que tener en cuenta algunos aspectos de la instalación, el mantenimiento y la durabilidad, así como la carga del viento.
3.0 Método de construcción

La torre de pruebas se construyó en las siguientes etapas:
- Excavación de un hoyo circular de 30 m de diámetro para la base de la torre. Tanto la excavación como la forma se lograron mediante una voladura inicial. Tras la excavación, el hoyo se aseguró con tirantes de anclaje y revestimiento de hormigón proyectado.
- Vertido de los cimientos de losas.
- Construcción de la estructura vertical de hormigón mediante encofrado deslizante. Todas las paredes se construyeron de forma continua durante un periodo de 4 meses.
- Construcción de las losas de forjado.
- Construcción de la zona de entrada.
4.0 Respuesta dinámica prevista a la carga del viento
Las frecuencias fundamentales para la torre de pruebas se predijeron en un intervalo de 0,17 Hz a 0,20 Hz en función de la etapa de construcción y del estado del hormigón (agrietado/sin agrietar), véase la figura 4.

El análisis del viento reveló que podía producirse una excitación resonante de la estructura a velocidades de viento que correspondían a valores del suelo (altura de 10 m) del orden de 55 a 60 km/h. Se preveía que, sin una amortiguación adicional, esta excitación resonante provocaría deflexiones en la parte superior de +/-750 mm, lo que no solo causaría molestias a los ocupantes, sino que también tendría importantes repercusiones en la fatiga de la estructura de hormigón de la torre (véase la figura 5). Para reducir la respuesta dinámica a la excitación del viento cruzado, se utilizó un sistema pasivo de amortiguadores de masas sintonizadas. Como la torre se iba a utilizar como torre de pruebas para construir equipos de ascensores sensibles a las oscilaciones, el propietario buscaba la posibilidad de someter la torre a una excitación artificial en días de calma, pero con desplazamientos que no causaran problemas de fatiga. El grado de movimiento de balanceo artificial solicitado se encontraba en el margen que se considera seguro de +/-200 mm. Esta solicitud dio la rara oportunidad de instalar un amortiguador de masa híbrido (HMD) o, dado que el sistema diseñado se desviaba de otros sistemas HMD instalados en el pasado, un denominado TMD de doble uso. El sistema se presentará en los siguientes capítulos, al igual que la optimización del sistema pasivo, el diseño del mecanismo de los actuadores, los algoritmos de control y el concepto de seguridad.

5.0 Optimización del sistema pasivo de amortiguadores de masas sintonizadas
Los parámetros del sistema de TMD pasivo debían determinarse teniendo en cuenta tres aspectos diferentes: a) proporcionar suficiente amortiguación estructural adicional para reducir la respuesta dinámica debida a la excitación por desprendimiento de vórtices, b) limitar el desplazamiento de la masa principal del TMD resultante en el modo pasivo a un valor alcanzable/práctico para cuando se vea sometido a una excitación por ráfagas de viento cruzado y c) elegir la masa del TMD en función del aporte de energía necesario para lograr la deflexión máxima deseada de la torre en el modo de excitación teniendo en cuenta la envolvente de rendimiento que permiten los actuadores suministrados (es decir, la fuerza máxima generada y la carrera máxima durante el funcionamiento). Para optimizar el sistema de TMD se utilizó un modelo numérico que representaba la distribución de la masa de la torre y los momentos de inercia de la masa según las propiedades estructurales identificadas. También se adaptaron los elementos de rigidez entre las plantas para que coincidieran con las formas modales y las frecuencias naturales de las observaciones a tamaño real. En la figura 6 de la izquierda se muestran las formas modales y las frecuencias naturales del modelo análogo empleado. En la figura 6 de la izquierda también se comparan las formas modales del modelo análogo con las del modelo detallado preparado por el asesor de estructuras.


Además, el TMD se modeló de forma diferenciada como un sistema pendular y teniendo en cuenta su posición excéntrica en la torre. Las características de carga para el caso de aportación dominante, es decir, la excitación resonante debida al desprendimiento de vórtices, son muy parecidas a las de una excitación armónica simple. Aun así, la carga de ráfaga coexistente es de naturaleza intrínsecamente estocástica, por lo que se aplican criterios de optimización distintos del conocido criterio de Den Hartog. Además, los desplazamientos relativos de la masa del TMD son mayores para una carga estocástica que para una carga de tipo armónico. Puesto que para la determinación numérica de los parámetros óptimos del TMD debe considerarse una carga cercana a la realidad, se generó un histórico temporal que incluía tanto la carga estocástica de ráfagas (basada en el espectro de Davenport) como una componente resonante superpuesta, similar al desprendimiento de vórtices, para representar la excitación general del viento cruzado (véase la fig. 3 derecha). En la figura 3 derecha se muestra la reducción de la deflexión de la torre que se puede lograr con el sistema de TMD pasivo, así como los desplazamientos de TMD resultantes.
A partir de estos resultados, para una amortiguación estructural inherente estimada de ξ=0,8 %, se determinó que el TMD debía tener una masa de 240 t para mantener los desplazamientos dentro de +/-650 mm y, al mismo tiempo, mantener una relación de amortiguación del TMD óptima para obtener el mejor rendimiento del TMD. Un incremento de la amortiguación del TMD podría haber reducido el desplazamiento sin que por ello la eficacia dejara de ser suficiente, pero esto habría afectado negativamente a los requisitos de fuerza del actuador. Para determinar las fuerzas necesarias para la configuración óptima del TMD de 240 t, se utilizó también el modelo análogo para constatar que, con una fuerza máxima de 40 kN de los actuadores, se pueden lograr deflexiones de la torre en el margen de +/-200 mm. En la figura 4 se muestran los resultados de una simulación numérica en el dominio del tiempo sobre el modelo numérico análogo; para ello, se muestran las deflexiones resultantes de la parte superior de la torre, las deflexiones de la masa del TMD y las fuerzas activas de entrada que las provocan.


6.0 Descripción del sistema de control
La dualidad del sistema de control tiene como objetivo a) reducir el consumo de energía durante el funcionamiento pasivo normal para disminuir las vibraciones que se producen y b) reducir los requisitos de fuerza de los actuadores al utilizar los efectos de resonancia con el fin de excitar la masa principal del TMD y lograr finalmente la demanda de fuerza real. Por lo tanto, en comparación con otros sistemas de control (véase la fig. 1), los actuadores conectan la estructura principal y la masa del TMD, pero no se utilizan para controlar la masa del TMD directamente, como sería el caso de un sistema de conductor/amortiguador de masa activa típico.
Para el TMD de doble uso instalado, se eligió una masa de reacción para el funcionamiento pasivo de 240 toneladas. Para el modo de funcionamiento de excitación, se acoplaron dos accionamientos lineales a la masa del TMD —uno en cada dirección principal— con pivotes cerca del centro de gravedad de la masa para evitar cualquier artefacto de torsión. Cada accionamiento lineal puede proporcionar fuerzas de hasta 40 kN dentro de una carrera de como máximo +/-600 mm (véase el detalle en la fig. 2). Los accionamientos lineales se pueden desmontar para que el modo pasivo no se vea influenciado por los rodamientos de los actuadores en el improbable caso de que se produzca un fallo en ellos.


Figura 10: Tipos de sistemas de control, comparación del TMD de doble uso con sistemas pasivos, semiactivos, activos e híbridos
El sistema está equipado con cuatro acelerómetros uniaxiales (K-Beam sísmico/MEMS; uno en cada dirección) para determinar el nivel superior de la torre y las aceleraciones de la masa del TMD. Las señales de aceleración se filtran por paso de banda en la gama de frecuencias naturales fundamentales de la torre (0,1 a 0,3 Hz) y se integran para obtener las velocidades y deflexiones de la torre.
Además, los valores de desplazamiento integrados pueden compararse con los de un sistema global de navegación por satélite complementario instalado también en la parte superior para comparar las derivas de la señal. Para ello, se realizó una primera prueba de correlación. Por otra parte, los desplazamientos del TMD son controlados directamente con transductores de potencia de cuerda y un sistema inductivo de medición de longitudes integrado en los motores lineales.
7.0 Algoritmo de control
El bucle de control general para la torre se muestra en la figura 5, donde se ilustra la secuencia de control en bucle cerrado. El diseño detallado del algoritmo de control requeriría modelos analíticos de la interacción entre los actuadores y la masa del TMD para determinar la conexión entre la entrada del actuador y la fuerza de acción aplicada. Estos deberían combinarse con el modelo analítico de la estructura principal que describe el comportamiento dinámico general del edificio. Además, en comparación con los algoritmos de control estándar que se utilizaron en otras aplicaciones de HMD como en [2],[3] o que se analizaron de manera teórica como en [1] el algoritmo de control para esta torre tuvo que tener en cuenta la excitación sincrónica controlada en una dirección principal y la reducción de la vibración en la dirección perpendicular. Dado que se espera que la respuesta dinámica se produzca principalmente en los modos fundamentales, podría aplicarse un control de retroalimentación lineal, con todas sus ventajas, para estas dos tareas a fin de evitar inestabilidades. Para llevar a cabo el control simple, el control de retroalimentación lineal, que atenúa la respuesta dinámica de las torres de forma perpendicular a la excitación, acciona el actuador correspondiente mediante una suma lineal ponderada especificada de siete mediciones dinámicas estructurales. Estas mediciones son: las aceleraciones del TMD y de la parte superior de la torre, las velocidades del TMD y de la parte superior de la torre, los desplazamientos del TMD y de la parte superior de la torre y el desplazamiento relativo del TMD a la parte superior de la torre.
Es importante señalar que los factores de ponderación preseleccionados son ganancias escalares simples, positivas o negativas. La parametrización de los factores de ponderación se basa en las pruebas dinámicas de la torre y no se aplica ninguna modificación dependiente de la frecuencia. La retroalimentación del actuador activo se calcula de manera instantánea (a 50 Hz) y es de nuevo una combinación lineal de las mediciones dinámicas anteriores. No se utiliza ninguna manipulación no lineal. El diseño de control también se puso a prueba en una simulación numérica en el dominio del tiempo (es decir, integración directa) para comprobar el rendimiento de la mitigación de las vibraciones del control del actuador. Para el modo de excitación se utilizó el mismo enfoque de control en combinación con un desplazamiento que representa la excitación de la torre hasta el valor de desplazamiento deseado. El desplazamiento es una función sinusoidal basada en la frecuencia fundamental captada en cada dirección. La salida de control destinada a contrarrestar la variación del desplazamiento superior debida a otras perturbaciones se modula entonces sobre la función de desplazamiento sinusoidal y el valor de control se adapta en consecuencia.

El control de retroalimentación lineal que reduce la respuesta dinámica de las torres de forma perpendicular a la excitación permite que la orden de fuerza para el actuador sea una suma lineal ponderada especificada de las siete mediciones dinámicas del programa. Estas siete mediciones son la aceleración del TMD y de la torre, la velocidad del TMD y de la torre, el desplazamiento del TMD y de la torre y el desplazamiento relativo del TMD a la torre. Es importante señalar que los factores de ponderación son valores escalares simples, positivos o negativos. La parametrización del factor de ponderación se basa en las pruebas dinámicas experimentales de la torre. La retroalimentación del actuador es activa y se calcula de forma instantánea (50 Hz),
mientras que los factores de ponderación son escalares y no utilizan ninguna forma de función de transferencia dependiente de la frecuencia. Además, la retroalimentación es una combinación lineal de la propiedad dinámica. No se aplica ninguna manipulación ni lógica no lineal. El diseño de control se desarrolló para una simulación numérica en el dominio del tiempo (integración directa), de manera que la entrada de fuerza se pudiera adaptar a la masa del TMD como control del actuador para cada paso de tiempo. En la figura 12 se muestran los resultados de la simulación para la supresión de vibraciones, los desplazamientos de la torre y el recorrido resultante de la masa del TMD.


Para el modo de excitación se utilizó el mismo enfoque de control en combinación con un desplazamiento que representa la excitación de la torre hasta el valor de desplazamiento deseado. El desplazamiento es una función sinusoidal basada en la frecuencia fundamental captada en cada dirección. La salida de control destinada a contrarrestar la variación del desplazamiento superior debida a las perturbaciones se modula entonces sobre la función de desplazamiento
sinusoidal y el valor de control se adapta en consecuencia. Para este desplazamiento se determinó un factor de ponderación experimental. En la figura 13 se muestran los resultados numéricos con la perturbación de la carga de ráfagas para el modo de excitación con una excitación sinusoidal simple y con la aplicación del algoritmo de control.


8.0 Concepto de seguridad
Teniendo en cuenta la fuerza de +/-40 kN que pueden proporcionar los accionamientos lineales que se utilizan como actuadores, es indispensable contar con un concepto de seguridad que garantice que los desplazamientos de la torre no superen las previsiones de fatiga. Esto es aplicable incluso aunque la salida de fuerza no sea suficiente para causar deflexiones superiores a los +/-200 mm predeterminados. Un modo de mejorar la seguridad del sistema era aumentar la redundancia de los sensores de control que registran la deflexión superior de la torre. La mejor manera de lograrlo es mediante un sistema de control adicional e independiente que, en el mejor de los casos, utilice un principio de medición diferente al del hardware de control. Para el proyecto que aquí se presenta, el hardware de control utilizó, como ya se ha mencionado, acelerómetros y un umbral de aceleración definido para el filtrado de paso de banda de la señal dentro del intervalo de las frecuencias naturales relevantes de la estructura. El sistema de control superior es un sistema global de navegación por satélite (GNSS, por sus siglas en inglés) con una precisión de +/-10 mm. Para el GNNS se necesita una estación base de referencia, que procesa los datos de coordenadas a los valores reales de respuesta de desplazamiento. Si el desplazamiento superior de la torre supera un umbral predeterminado durante el modo de excitación artificial, lo que podría deberse a un viento adicional u otra excitación, un relé cambiará la señal a 0 V. Esto provocará la interrupción del modo de excitación. Además, ambos sistemas de control comprueban constantemente los datos obtenidos en busca de señales erróneas de los sensores, lo que también provocará la interrupción del modo de excitación activo. Las señales de aceleración/potencia erróneas se detectarán mediante un criterio de detección de picos espectrales; solo podrá asumirse que los sensores proporcionan señales legítimas si es posible detectar picos en un margen relevante. Cuando el GNNS analiza el cambio de los datos de coordenadas, si los datos recogidos no cambian en el momento oportuno, se asumirá automáticamente que la señal es errónea.
9.0 Pruebas de vibración
Las pruebas de vibración iniciales de la torre se efectuaron en la fase actual, en la que la torre aún no está terminada, por lo que las frecuencias fundamentales de la torre en esta fase están por encima del margen de sintonización especificado en el sistema de TMD pasivo. El TMD está adaptado a la frecuencia de sintonización más alta posible. El objetivo de las pruebas de vibración era determinar las frecuencias fundamentales de la torre con el sistema de TMD bloqueado, así como la amortiguación estructural inherente. También debía determinarse el comportamiento dinámico con el sistema TMD pasivo acoplado, así como el aumento de la amortiguación estructural debido al sistema de TMD pasivo. Para identificar las frecuencias naturales fundamentales de la torre se puede utilizar el método de la densidad espectral de potencia normalizada promediada [1] (ANPSD, por sus siglas en inglés). Para ello, es necesario separar en segmentos los históricos temporales registrados. Estos segmentos deben transformarse en el dominio de la frecuencia. Los espectros obtenidos deben normalizarse, promediarse y multiplicarse por el espectro complejo conjugado.
De este modo, se eliminarán todas las vibraciones aleatorias y solo se mostrarán las vibraciones libres recurrentes de la estructura en el espectro promediado, que ahora representa las frecuencias naturales excitadas de forma dominante en la torre. En la figura 14 izquierda se muestran los históricos temporales registrados de las vibraciones ambientales horizontales en las direcciones x e y con el TMD bloqueado. En la figura 14 derecha se muestran los espectros de potencia automática promediados obtenidos para una longitud de segmento de 120 s. Los espectros indican que la torre presenta una respuesta dinámica en dos frecuencias dominantes (0,225 Hz en la dirección x y 0,245 Hz en la dirección y).
Además del método del espectro de potencia promediado descrito anteriormente —que parte del supuesto de que la excitación ambiental provoca una respuesta dinámica suficiente en los modos de vibración de interés para obtener seguridad estocástica—, las frecuencias naturales se determinaron con el software comercial de procesamiento de señales ARTEMIS, [1] que incorpora el método de descomposición mejorada en el dominio de la frecuencia y el de identificación del subespacio estocástico.

La descomposición mejorada en el dominio de la frecuencia (EFDD, por sus siglas en inglés) y la identificación del subespacio estocástico son técnicas ampliamente utilizadas para la identificación de parámetros modales solo de salida.


El método EFDD se basa en el cálculo de los espectros de respuesta. Por lo tanto, se necesitan registros extensos para mantener bajo el error en la estimación del espectro y para extraer los parámetros modales de forma fiable. El algoritmo de identificación del subespacio estocástico se aplicó para identificar los puentes con un modelo de solo salida. Los métodos de identificación del subespacio estocástico funcionan en el dominio del tiempo y se basan en una descripción del espacio de estados del problema dinámico. Los resultados de la identificación del sistema en diferentes órdenes del modelo se comparan para distinguir los verdaderos modos estructurales de los modos espurios en los denominados diagramas de estabilización. Estos diagramas son una forma popular de seleccionar el modelo del sistema identificado, ya que los modos estructurales verdaderos tienden a ser estables para órdenes de modelo sucesivos y cumplen determinados criterios de estabilización que se evalúan en un procedimiento automatizado. La figura 15 presenta la tarjeta de estabilidad correspondiente a los datos ambientales registrados, a partir de la cual se han podido determinar los modos pertinentes. En la figura 14 también se muestran los modos identificados y las relaciones de amortiguación determinadas para cada modo con el TMD bloqueado (izquierda) y el TMD activado (derecha). Se observa un aumento de la amortiguación estructural. La amortiguación estructural adicional está en el intervalo de un valor teórico que puede determinarse a partir del modelo teórico para el que se consideró la configuración del TMD desintonizado.
Además de las pruebas de vibración ambiental con el sistema de TMD pasivo, se realizaron pruebas preliminares con el modo de excitación activo a pesar del estado desintonizado del sistema de TMD. En la figura 12 izquierda se muestra el histórico temporal de las aceleraciones registradas en la parte superior de la torre. Después de una excitación sinusoidal inicial, se habilitó el algoritmo para un grado de aceleración constante con el fin de determinar de forma experimental la correlación existente entre la deflexión de la torre y el desplazamiento forzado de la masa del TMD. El histórico temporal que se muestra en la figura 12 presenta los dos escenarios de prueba en el modo de excitación, y los espectros FFT correspondientes indican la evidente respuesta de la torre en sus dos frecuencias fundamentales (dirección x e y). El tramo de tiempo marcado en verde corresponde a una excitación sinusoidal de la masa con el control activo desactivado que provocó una respuesta dinámica en ambas direcciones principales. El espectro FFT resultante indica los dos picos que identifican las frecuencias fundamentales en estas dos direcciones. El fragmento de tiempo marcado en azul corresponde a una excitación con control activo habilitado que provocó un desplazamiento de la torre más estable con predominio de una dirección. El decaimiento de la vibración resultante después de desactivar el modo de excitación también se utilizó para determinar la amortiguación estructural y se determinó que era D = 2,4 %. Este resultado coincide con la relación de amortiguación determinada con los algoritmos SSI.

10.0 Conclusión y perspectivas
En la torre de pruebas de Thyssen Krupp, de 246 m de altura, se instaló un TMD de doble uso con el objetivo de someter a la torre a una respuesta dinámica controlada en sus frecuencias fundamentales. El objetivo de esta excitación es lograr un balanceo definido del edificio en las dos direcciones principales de la torre. A partir de los cálculos numéricos se determinó que el TMD debía tener una masa de 240 t para lograr la amortiguación suplementaria necesaria para el modo pasivo y generar la fuerza de control necesaria para lograr el desplazamiento superior de la torre de +/-200 mm. Para generar un desplazamiento estable para el modo de excitación y suprimir los desplazamientos causados por el viento y la componente de vibración forzada en la dirección perpendicular, se desarrolló un algoritmo de control que se probó con simulaciones numéricas. Después de instalar el sistema de TMD de tipo péndulo pasivo, para el que se utilizaron losas de hormigón prefabricadas como masa de reacción, se pusieron en marcha los actuadores y se realizaron las primeras pruebas. Las pruebas revelaron que la amortiguación inherente de la torre era más alta de lo previsto, pero todos los modos relevantes pudieron determinarse con precisión. El modo de excitación activa del edificio funcionaba y pudo probarse, aunque no en toda su extensión para derivar todos los parámetros de funcionamiento, ya que el edificio aún no está totalmente terminado. Debido al estado prematuro del edificio, el TMD pasivo no pudo adaptarse a las frecuencias fundamentales determinadas.
Una vez adaptado el sistema TMD, se llevarán a cabo nuevas pruebas en el edificio, entre las que se incluirán también pruebas relativas a la amortiguación dependiente de la amplitud y a la integridad del concepto de seguridad.
REFERENCIAS
[1] Wenzel, H.; Pichler, D.; Schedler, R. (1991). «Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken», Bauingenieur 74
[2] Döhler, M.; Andersen, P.: Mevel, L. (2012). «Operational Modal Analysis using a Fast Stochastic Subspace Identification Method», Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T.; Spencer, J.R. (2000). «Active, Semi-Active and hybrid control of structures» In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199-1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437-446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655-1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24-29.
[8] Soong, T.T. «Active Structural Control: Theory and Practice»; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A.; Kazuto, S. (2008). «Active Control of Structures», Wiley, Padstow
1.0 Introducción, antecedentes
En el suroeste de Alemania, se ha erigido una torre de 246 m de altura para acoger un centro de pruebas de innovaciones para ascensores. La torre tiene una superficie circular de 20 m de diámetro y ofrece espacio para 9 huecos de ascensor de prueba, un ascensor de servicio contra incendios y un ascensor con vista panorámica de cristal. Además, se ha previsto un hueco de 220 m que se utilizará como hueco de elevación mecánica para garantizar los programas de pruebas.
La base de la torre tiene un diámetro de 40 m para disponer de espacio adicional para las instalaciones de servicio, un vestíbulo y un centro educativo. A una altura de 232 m, una plataforma de observación —la más alta de Alemania— permite disfrutar de una vista espectacular de la Selva Negra e incluso de los Alpes en días claros.

2.0 Sistema estructural
El sistema estructural de la torre de pruebas consiste básicamente en un tubo de hormigón armado de 20,8 m de diámetro que se hunde 30 metros en el suelo circundante (véase la figura 2). Hasta una altura de 110 m, el tubo tiene un espesor de 40 cm, por encima, de 25 cm. El suelo, compuesto por una capa de Keuper y piedra caliza de concha subyacente, proporciona una gran capacidad de carga, por lo que no fue necesaria la cimentación con pilotes. Además de la sujeción por el suelo circundante, la estructura más ancha de la base de la torre proporciona una rigidez lateral adicional.
La rigidez interna del tubo de hormigón se debe principalmente a las paredes interiores de los huecos de ascensor. Solo en determinadas alturas se instalaron losas de techo prefabricadas para permitir el acceso a los huecos de ascensor. Algunos de los huecos de ascensor terminan a una altura de 115 m y están cubiertos por suelos de vano largo de 40 cm de espesor que se colocaron allí mismo. Estas plantas están destinadas a oficinas. Por encima, hay un espacio vacío hasta la altura de 197 m que se utiliza como depósito de calor y para el sistema de TMD. La parte superior de la torre se destina a oficinas y al resto de los huecos de ascensor.

Una característica distintiva de la torre de pruebas es la fachada textil, que consiste en una malla de fibra de vidrio recubierta de PTFE. La anchura de la malla aumenta con la altura del edificio para potenciar la translucidez de la fachada, disminuir la densidad y el peso del material y lograr efectos aerodinámicos.
La forma de espiral de la fachada está concebida para funcionar como una espiral de Scruton y el propio tejido ayuda a dar sombra a la estructura de hormigón para evitar tensiones térmicas inducidas por la radiación solar. Para el diseño de la fachada y la elección del material, hubo que tener en cuenta algunos aspectos de la instalación, el mantenimiento y la durabilidad, así como la carga del viento.
3.0 Método de construcción

La torre de pruebas se construyó en las siguientes etapas:
- Excavación de un hoyo circular de 30 m de diámetro para la base de la torre. Tanto la excavación como la forma se lograron mediante una voladura inicial. Tras la excavación, el hoyo se aseguró con tirantes de anclaje y revestimiento de hormigón proyectado.
- Vertido de los cimientos de losas.
- Construcción de la estructura vertical de hormigón mediante encofrado deslizante. Todas las paredes se construyeron de forma continua durante un periodo de 4 meses.
- Construcción de las losas de forjado.
- Construcción de la zona de entrada.
4.0 Respuesta dinámica prevista a la carga del viento
Las frecuencias fundamentales para la torre de pruebas se predijeron en un intervalo de 0,17 Hz a 0,20 Hz en función de la etapa de construcción y del estado del hormigón (agrietado/sin agrietar), véase la figura 4.

El análisis del viento reveló que podía producirse una excitación resonante de la estructura a velocidades de viento que correspondían a valores del suelo (altura de 10 m) del orden de 55 a 60 km/h. Se preveía que, sin una amortiguación adicional, esta excitación resonante provocaría deflexiones en la parte superior de +/-750 mm, lo que no solo causaría molestias a los ocupantes, sino que también tendría importantes repercusiones en la fatiga de la estructura de hormigón de la torre (véase la figura 5). Para reducir la respuesta dinámica a la excitación del viento cruzado, se utilizó un sistema pasivo de amortiguadores de masas sintonizadas. Como la torre se iba a utilizar como torre de pruebas para construir equipos de ascensores sensibles a las oscilaciones, el propietario buscaba la posibilidad de someter la torre a una excitación artificial en días de calma, pero con desplazamientos que no causaran problemas de fatiga. El grado de movimiento de balanceo artificial solicitado se encontraba en el margen que se considera seguro de +/-200 mm. Esta solicitud dio la rara oportunidad de instalar un amortiguador de masa híbrido (HMD) o, dado que el sistema diseñado se desviaba de otros sistemas HMD instalados en el pasado, un denominado TMD de doble uso. El sistema se presentará en los siguientes capítulos, al igual que la optimización del sistema pasivo, el diseño del mecanismo de los actuadores, los algoritmos de control y el concepto de seguridad.

5.0 Optimización del sistema pasivo de amortiguadores de masas sintonizadas
Los parámetros del sistema de TMD pasivo debían determinarse teniendo en cuenta tres aspectos diferentes: a) proporcionar suficiente amortiguación estructural adicional para reducir la respuesta dinámica debida a la excitación por desprendimiento de vórtices, b) limitar el desplazamiento de la masa principal del TMD resultante en el modo pasivo a un valor alcanzable/práctico para cuando se vea sometido a una excitación por ráfagas de viento cruzado y c) elegir la masa del TMD en función del aporte de energía necesario para lograr la deflexión máxima deseada de la torre en el modo de excitación teniendo en cuenta la envolvente de rendimiento que permiten los actuadores suministrados (es decir, la fuerza máxima generada y la carrera máxima durante el funcionamiento). Para optimizar el sistema de TMD se utilizó un modelo numérico que representaba la distribución de la masa de la torre y los momentos de inercia de la masa según las propiedades estructurales identificadas. También se adaptaron los elementos de rigidez entre las plantas para que coincidieran con las formas modales y las frecuencias naturales de las observaciones a tamaño real. En la figura 6 de la izquierda se muestran las formas modales y las frecuencias naturales del modelo análogo empleado. En la figura 6 de la izquierda también se comparan las formas modales del modelo análogo con las del modelo detallado preparado por el asesor de estructuras.


Además, el TMD se modeló de forma diferenciada como un sistema pendular y teniendo en cuenta su posición excéntrica en la torre. Las características de carga para el caso de aportación dominante, es decir, la excitación resonante debida al desprendimiento de vórtices, son muy parecidas a las de una excitación armónica simple. Aun así, la carga de ráfaga coexistente es de naturaleza intrínsecamente estocástica, por lo que se aplican criterios de optimización distintos del conocido criterio de Den Hartog. Además, los desplazamientos relativos de la masa del TMD son mayores para una carga estocástica que para una carga de tipo armónico. Puesto que para la determinación numérica de los parámetros óptimos del TMD debe considerarse una carga cercana a la realidad, se generó un histórico temporal que incluía tanto la carga estocástica de ráfagas (basada en el espectro de Davenport) como una componente resonante superpuesta, similar al desprendimiento de vórtices, para representar la excitación general del viento cruzado (véase la fig. 3 derecha). En la figura 3 derecha se muestra la reducción de la deflexión de la torre que se puede lograr con el sistema de TMD pasivo, así como los desplazamientos de TMD resultantes. A partir de estos resultados, para una amortiguación estructural inherente estimada de ξ=0,8 %, se determinó que el TMD debía tener una masa de 240 t para mantener los desplazamientos dentro de +/-650 mm y, al mismo tiempo, mantener una relación de amortiguación del TMD óptima para obtener el mejor rendimiento del TMD. Un incremento de la amortiguación del TMD podría haber reducido el desplazamiento sin que por ello la eficacia dejara de ser suficiente, pero esto habría afectado negativamente a los requisitos de fuerza del actuador. Para determinar las fuerzas necesarias para la configuración óptima del TMD de 240 t, se utilizó también el modelo análogo para constatar que, con una fuerza máxima de 40 kN de los actuadores, se pueden lograr deflexiones de la torre en el margen de +/-200 mm. En la figura 4 se muestran los resultados de una simulación numérica en el dominio del tiempo sobre el modelo numérico análogo; para ello, se muestran las deflexiones resultantes de la parte superior de la torre, las deflexiones de la masa del TMD y las fuerzas activas de entrada que las provocan.


6.0 Descripción del sistema de control
La dualidad del sistema de control tiene como objetivo a) reducir el consumo de energía durante el funcionamiento pasivo normal para disminuir las vibraciones que se producen y b) reducir los requisitos de fuerza de los actuadores al utilizar los efectos de resonancia con el fin de excitar la masa principal del TMD y lograr finalmente la demanda de fuerza real. Por lo tanto, en comparación con otros sistemas de control (véase la fig. 1), los actuadores conectan la estructura principal y la masa del TMD, pero no se utilizan para controlar la masa del TMD directamente, como sería el caso de un sistema de conductor/amortiguador de masa activa típico. Para el TMD de doble uso instalado, se eligió una masa de reacción para el funcionamiento pasivo de 240 toneladas. Para el modo de funcionamiento de excitación, se acoplaron dos accionamientos lineales a la masa del TMD —uno en cada dirección principal— con pivotes cerca del centro de gravedad de la masa para evitar cualquier artefacto de torsión. Cada accionamiento lineal puede proporcionar fuerzas de hasta 40 kN dentro de una carrera de como máximo +/-600 mm (véase el detalle en la fig. 2). Los accionamientos lineales se pueden desmontar para que el modo pasivo no se vea influenciado por los rodamientos de los actuadores en el improbable caso de que se produzca un fallo en ellos.


El sistema está equipado con cuatro acelerómetros uniaxiales (K-Beam sísmico/MEMS; uno en cada dirección) para determinar el nivel superior de la torre y las aceleraciones de la masa del TMD. Las señales de aceleración se filtran por paso de banda en la gama de frecuencias naturales fundamentales de la torre (0,1 a 0,3 Hz) y se integran para obtener las velocidades y deflexiones de la torre. Además, los valores de desplazamiento integrados pueden compararse con los de un sistema global de navegación por satélite complementario instalado también en la parte superior para comparar las derivas de la señal. Para ello, se realizó una primera prueba de correlación. Por otra parte, los desplazamientos del TMD son controlados directamente con transductores de potencia de cuerda y un sistema inductivo de medición de longitudes integrado en los motores lineales.
7.0 Algoritmo de control
El bucle de control general para la torre se muestra en la figura 5, donde se ilustra la secuencia de control en bucle cerrado. El diseño detallado del algoritmo de control requeriría modelos analíticos de la interacción entre los actuadores y la masa del TMD para determinar la conexión entre la entrada del actuador y la fuerza de acción aplicada. Estos deberían combinarse con el modelo analítico de la estructura principal que describe el comportamiento dinámico general del edificio. Además, en comparación con los algoritmos de control estándar que se utilizaron en otras aplicaciones de HMD como en [2],[3] o que se analizaron de manera teórica como en [1] el algoritmo de control para esta torre tuvo que tener en cuenta la excitación sincrónica controlada en una dirección principal y la reducción de la vibración en la dirección perpendicular. Dado que se espera que la respuesta dinámica se produzca principalmente en los modos fundamentales, podría aplicarse un control de retroalimentación lineal, con todas sus ventajas, para estas dos tareas a fin de evitar inestabilidades. Para llevar a cabo el control simple, el control de retroalimentación lineal, que atenúa la respuesta dinámica de las torres de forma perpendicular a la excitación, acciona el actuador correspondiente mediante una suma lineal ponderada especificada de siete mediciones dinámicas estructurales. Estas mediciones son: las aceleraciones del TMD y de la parte superior de la torre, las velocidades del TMD y de la parte superior de la torre, los desplazamientos del TMD y de la parte superior de la torre y el desplazamiento relativo del TMD a la parte superior de la torre. Es importante señalar que los factores de ponderación preseleccionados son ganancias escalares simples, positivas o negativas. La parametrización de los factores de ponderación se basa en las pruebas dinámicas de la torre y no se aplica ninguna modificación dependiente de la frecuencia. La retroalimentación del actuador activo se calcula de manera instantánea (a 50 Hz) y es de nuevo una combinación lineal de las mediciones dinámicas anteriores. No se utiliza ninguna manipulación no lineal. El diseño de control también se puso a prueba en una simulación numérica en el dominio del tiempo (es decir, integración directa) para comprobar el rendimiento de la mitigación de las vibraciones del control del actuador. Para el modo de excitación se utilizó el mismo enfoque de control en combinación con un desplazamiento que representa la excitación de la torre hasta el valor de desplazamiento deseado. El desplazamiento es una función sinusoidal basada en la frecuencia fundamental captada en cada dirección. La salida de control destinada a contrarrestar la variación del desplazamiento superior debida a otras perturbaciones se modula entonces sobre la función de desplazamiento sinusoidal y el valor de control se adapta en consecuencia.

El control de retroalimentación lineal que reduce la respuesta dinámica de las torres de forma perpendicular a la excitación permite que la orden de fuerza para el actuador sea una suma lineal ponderada especificada de las siete mediciones dinámicas del programa. Estas siete mediciones son la aceleración del TMD y de la torre, la velocidad del TMD y de la torre, el desplazamiento del TMD y de la torre y el desplazamiento relativo del TMD a la torre. Es importante señalar que los factores de ponderación son valores escalares simples, positivos o negativos. La parametrización del factor de ponderación se basa en las pruebas dinámicas experimentales de la torre. La retroalimentación del actuador es activa y se calcula de forma instantánea (50 Hz), mientras que los factores de ponderación son escalares y no utilizan ninguna forma de función de transferencia dependiente de la frecuencia. Además, la retroalimentación es una combinación lineal de la propiedad dinámica. No se aplica ninguna manipulación ni lógica no lineal. El diseño de control se desarrolló para una simulación numérica en el dominio del tiempo (integración directa), de manera que la entrada de fuerza se pudiera adaptar a la masa del TMD como control del actuador para cada paso de tiempo. En la figura 12 se muestran los resultados de la simulación para la supresión de vibraciones, los desplazamientos de la torre y el recorrido resultante de la masa del TMD.


Para el modo de excitación se utilizó el mismo enfoque de control en combinación con un desplazamiento que representa la excitación de la torre hasta el valor de desplazamiento deseado. El desplazamiento es una función sinusoidal basada en la frecuencia fundamental captada en cada dirección. La salida de control destinada a contrarrestar la variación del desplazamiento superior debida a las perturbaciones se modula entonces sobre la función de desplazamiento sinusoidal y el valor de control se adapta en consecuencia. Para este desplazamiento se determinó un factor de ponderación experimental. En la figura 13 se muestran los resultados numéricos con la perturbación de la carga de ráfagas para el modo de excitación con una excitación sinusoidal simple y con la aplicación del algoritmo de control.


8.0 Concepto de seguridad
Teniendo en cuenta la fuerza de +/-40 kN que pueden proporcionar los accionamientos lineales que se utilizan como actuadores, es indispensable contar con un concepto de seguridad que garantice que los desplazamientos de la torre no superen las previsiones de fatiga. Esto es aplicable incluso aunque la salida de fuerza no sea suficiente para causar deflexiones superiores a los +/-200 mm predeterminados. Un modo de mejorar la seguridad del sistema era aumentar la redundancia de los sensores de control que registran la deflexión superior de la torre. La mejor manera de lograrlo es mediante un sistema de control adicional e independiente que, en el mejor de los casos, utilice un principio de medición diferente al del hardware de control. Para el proyecto que aquí se presenta, el hardware de control utilizó, como ya se ha mencionado, acelerómetros y un umbral de aceleración definido para el filtrado de paso de banda de la señal dentro del intervalo de las frecuencias naturales relevantes de la estructura. El sistema de control superior es un sistema global de navegación por satélite (GNSS, por sus siglas en inglés) con una precisión de +/-10 mm. Para el GNNS se necesita una estación base de referencia, que procesa los datos de coordenadas a los valores reales de respuesta de desplazamiento. Si el desplazamiento superior de la torre supera un umbral predeterminado durante el modo de excitación artificial, lo que podría deberse a un viento adicional u otra excitación, un relé cambiará la señal a 0 V. Esto provocará la interrupción del modo de excitación. Además, ambos sistemas de control comprueban constantemente los datos obtenidos en busca de señales erróneas de los sensores, lo que también provocará la interrupción del modo de excitación activo. Las señales de aceleración/potencia erróneas se detectarán mediante un criterio de detección de picos espectrales; solo podrá asumirse que los sensores proporcionan señales legítimas si es posible detectar picos en un margen relevante. Cuando el GNNS analiza el cambio de los datos de coordenadas, si los datos recogidos no cambian en el momento oportuno, se asumirá automáticamente que la señal es errónea.
9.0 Pruebas de vibración
Las pruebas de vibración iniciales de la torre se efectuaron en la fase actual, en la que la torre aún no está terminada, por lo que las frecuencias fundamentales de la torre en esta fase están por encima del margen de sintonización especificado en el sistema de TMD pasivo. El TMD está adaptado a la frecuencia de sintonización más alta posible. El objetivo de las pruebas de vibración era determinar las frecuencias fundamentales de la torre con el sistema de TMD bloqueado, así como la amortiguación estructural inherente. También debía determinarse el comportamiento dinámico con el sistema TMD pasivo acoplado, así como el aumento de la amortiguación estructural debido al sistema de TMD pasivo. Para identificar las frecuencias naturales fundamentales de la torre se puede utilizar el método de la densidad espectral de potencia normalizada promediada [1] (ANPSD, por sus siglas en inglés). Para ello, es necesario separar en segmentos los históricos temporales registrados. Estos segmentos deben transformarse en el dominio de la frecuencia. Los espectros obtenidos deben normalizarse, promediarse y multiplicarse por el espectro complejo conjugado.
De este modo, se eliminarán todas las vibraciones aleatorias y solo se mostrarán las vibraciones libres recurrentes de la estructura en el espectro promediado, que ahora representa las frecuencias naturales excitadas de forma dominante en la torre. En la figura 14 izquierda se muestran los históricos temporales registrados de las vibraciones ambientales horizontales en las direcciones x e y con el TMD bloqueado. En la figura 14 derecha se muestran los espectros de potencia automática promediados obtenidos para una longitud de segmento de 120 s. Los espectros indican que la torre presenta una respuesta dinámica en dos frecuencias dominantes (0,225 Hz en la dirección x y 0,245 Hz en la dirección y).
Además del método del espectro de potencia promediado descrito anteriormente —que parte del supuesto de que la excitación ambiental provoca una respuesta dinámica suficiente en los modos de vibración de interés para obtener seguridad estocástica—, las frecuencias naturales se determinaron con el software comercial de procesamiento de señales ARTEMIS, [1] que incorpora el método de descomposición mejorada en el dominio de la frecuencia y el de identificación del subespacio estocástico.

La descomposición mejorada en el dominio de la frecuencia (EFDD, por sus siglas en inglés) y la identificación del subespacio estocástico son técnicas ampliamente utilizadas para la identificación de parámetros modales solo de salida.


El método EFDD se basa en el cálculo de los espectros de respuesta. Por lo tanto, se necesitan registros extensos para mantener bajo el error en la estimación del espectro y para extraer los parámetros modales de forma fiable. El algoritmo de identificación del subespacio estocástico se aplicó para identificar los puentes con un modelo de solo salida. Los métodos de identificación del subespacio estocástico funcionan en el dominio del tiempo y se basan en una descripción del espacio de estados del problema dinámico. Los resultados de la identificación del sistema en diferentes órdenes del modelo se comparan para distinguir los verdaderos modos estructurales de los modos espurios en los denominados diagramas de estabilización. Estos diagramas son una forma popular de seleccionar el modelo del sistema identificado, ya que los modos estructurales verdaderos tienden a ser estables para órdenes de modelo sucesivos y cumplen determinados criterios de estabilización que se evalúan en un procedimiento automatizado. La figura 15 presenta la tarjeta de estabilidad correspondiente a los datos ambientales registrados, a partir de la cual se han podido determinar los modos pertinentes. En la figura 14 también se muestran los modos identificados y las relaciones de amortiguación determinadas para cada modo con el TMD bloqueado (izquierda) y el TMD activado (derecha). Se observa un aumento de la amortiguación estructural. La amortiguación estructural adicional está en el intervalo de un valor teórico que puede determinarse a partir del modelo teórico para el que se consideró la configuración del TMD desintonizado. Además de las pruebas de vibración ambiental con el sistema de TMD pasivo, se realizaron pruebas preliminares con el modo de excitación activo a pesar del estado desintonizado del sistema de TMD. En la figura 12 izquierda se muestra el histórico temporal de las aceleraciones registradas en la parte superior de la torre. Después de una excitación sinusoidal inicial, se habilitó el algoritmo para un grado de aceleración constante con el fin de determinar de forma experimental la correlación existente entre la deflexión de la torre y el desplazamiento forzado de la masa del TMD. El histórico temporal que se muestra en la figura 12 presenta los dos escenarios de prueba en el modo de excitación, y los espectros FFT correspondientes indican la evidente respuesta de la torre en sus dos frecuencias fundamentales (dirección x e y). El tramo de tiempo marcado en verde corresponde a una excitación sinusoidal de la masa con el control activo desactivado que provocó una respuesta dinámica en ambas direcciones principales. El espectro FFT resultante indica los dos picos que identifican las frecuencias fundamentales en estas dos direcciones. El fragmento de tiempo marcado en azul corresponde a una excitación con control activo habilitado que provocó un desplazamiento de la torre más estable con predominio de una dirección. El decaimiento de la vibración resultante después de desactivar el modo de excitación también se utilizó para determinar la amortiguación estructural y se determinó que era D = 2,4 %. Este resultado coincide con la relación de amortiguación determinada con los algoritmos SSI.

10.0 Conclusión y perspectivas
En la torre de pruebas de Thyssen Krupp, de 246 m de altura, se instaló un TMD de doble uso con el objetivo de someter a la torre a una respuesta dinámica controlada en sus frecuencias fundamentales. El objetivo de esta excitación es lograr un balanceo definido del edificio en las dos direcciones principales de la torre. A partir de los cálculos numéricos se determinó que el TMD debía tener una masa de 240 t para lograr la amortiguación suplementaria necesaria para el modo pasivo y generar la fuerza de control necesaria para lograr el desplazamiento superior de la torre de +/-200 mm. Para generar un desplazamiento estable para el modo de excitación y suprimir los desplazamientos causados por el viento y la componente de vibración forzada en la dirección perpendicular, se desarrolló un algoritmo de control que se probó con simulaciones numéricas. Después de instalar el sistema de TMD de tipo péndulo pasivo, para el que se utilizaron losas de hormigón prefabricadas como masa de reacción, se pusieron en marcha los actuadores y se realizaron las primeras pruebas. Las pruebas revelaron que la amortiguación inherente de la torre era más alta de lo previsto, pero todos los modos relevantes pudieron determinarse con precisión. El modo de excitación activa del edificio funcionaba y pudo probarse, aunque no en toda su extensión para derivar todos los parámetros de funcionamiento, ya que el edificio aún no está totalmente terminado. Debido al estado prematuro del edificio, el TMD pasivo no pudo adaptarse a las frecuencias fundamentales determinadas.
Una vez adaptado el sistema TMD, se llevarán a cabo nuevas pruebas en el edificio, entre las que se incluirán también pruebas relativas a la amortiguación dependiente de la amplitud y a la integridad del concepto de seguridad.
REFERENCIAS
[1] Wenzel, H.; Pichler, D.; Schedler, R. (1991). «Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken», Bauingenieur 74
[2] Döhler, M.; Andersen, P.: Mevel, L. (2012). «Operational Modal Analysis using a Fast Stochastic Subspace Identification Method», Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T.; Spencer, J.R. (2000). «Active, Semi-Active and hybrid control of structures» In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199-1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437-446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655-1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24-29.
[8] Soong, T.T. «Active Structural Control: Theory and Practice»; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A.; Kazuto, S. (2008). «Active Control of Structures», Wiley, Padstow
Compartir este post
Otros recursos
¿Desea recibir más información acerca de este tema?
Póngase en contacto con nosotros para hacernos llegar su consulta.
Uno de nuestros ingenieros de proyectos se pondrá en contacto con usted en breve.
Otros recursos
¿Desea recibir más información acerca de este tema?
Póngase en contacto con nosotros para hacernos llegar su consulta.
Uno de nuestros ingenieros de proyectos se pondrá en contacto con usted en breve.